


best of, Life, politics, sociology
Uber’s locational pricing

NVMe SSD and sleep
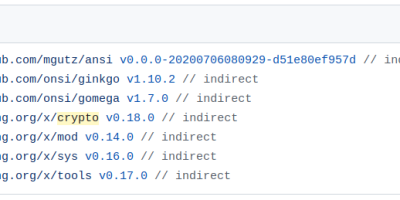
Why does golines need crypto?
Tiling window mangers!

Turning the power button LED off.

Vi(m) it is

The ThinkPad pointer

Home updates user impact survey.
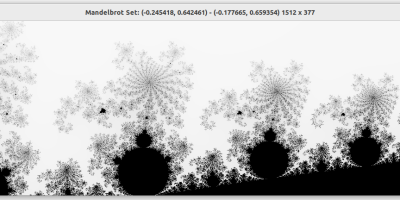
golang (7): parallelization

golang (6): Profiling

ThinkPad E14: Final verdict: Two thumbs up

Upgrading the old x220

Linux: pdf manipulations (+printing and scanning)

ThinkPad E14 field run

4D recap

golang (5): tangled up in slices

coding diary, Life, politics, sociology
Ubuntu on a ThinkPad

golang (4): methods
